小时候提梦想大家都会夸你懂事,
长大后提梦想大家都会说你幼稚。
开盲盒看博客
这几天迷上了通过虫洞随机访问一些小众的个人博客。感觉就像免费开盲盒,时不时的会发现几个宝藏网站。
这其实是十年之约的一个附加功能。类似的项目还有几个,不过十年对成员的要求最包容,最自由。不需要把上面的图标加载在主页上。
计算圆周率的神仙代码
#include <stdio.h>
long a=10000,b=0,c=10000,d,e,f[10001],g;
int main(){
for(;b != c; f[b++] = a/5);
for(; d=0,g=c*2,c>5000; c--,printf("%.4d",e+d/a),e=d%a)
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
return 0;
}这段代码是一个使用 C 语言编写的计算圆周率的程序。它使用了一个经典的算法,叫做Bailey-Borwein-Plouffe公式来计算圆周率的十进制表示。
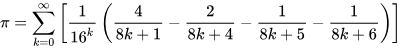
这段代码的运行结果是打印出圆周率的前10000位小数。
该算法的核心思想是利用无限级数的性质,通过不断迭代来逼近圆周率的值。具体算法如下:
- 初始化变量a、b、c、d、e、f和g。
- 进行第一个循环,从0到c,将a/5的结果保存在数组f中。
- 进行第二个循环,从c到5000,迭代计算圆周率的小数位数。
- 在循环中,首先计算d的值,然后更新f数组中的元素。
- 最后,打印出当前计算的小数位数。
这段代码使用了一些技巧来提高计算速度,比如使用了位运算、迭代代替递归等。但是这种优化方式使代码的可读性变差,也增加了代码的复杂性。使用这段代码可以得到圆周率的前10000位小数,但由于浮点数的精度限制,结果可能并不完全准确。
上面的介绍来自Chatgpt,我是完全没听懂。
最后来上几张图片大家轻松一下







